The Adventures of Cannon Man

Have you heard about Function Carnival created by Desmos, Christopher Danielson and Dan Meyer? The basic concept is this:

Students watch a video. They try to graph what they see. Then they play back the video and see how their graphical model would be represented as an animation. Does what they meant to graph about the world actually match the world?

Looking at it for the first time it appeared that the three graphing activities had very specific aims. But, for some reason, I was curious how it might play out with the elementary set.

I showed my eight year old the first activity, Cannon Man, after school on Monday and we did not stop for over 45 minutes. At first she tried to solve the graph and was working really hard, with great conversations between the two of us ('cause I'm still new to all this too, plus we're pretty good at learning stuff together sometimes). At one point she said, "Just show me the answer!" and I said, "Well, that's the point, it's you who figures out what the answer is."   

 

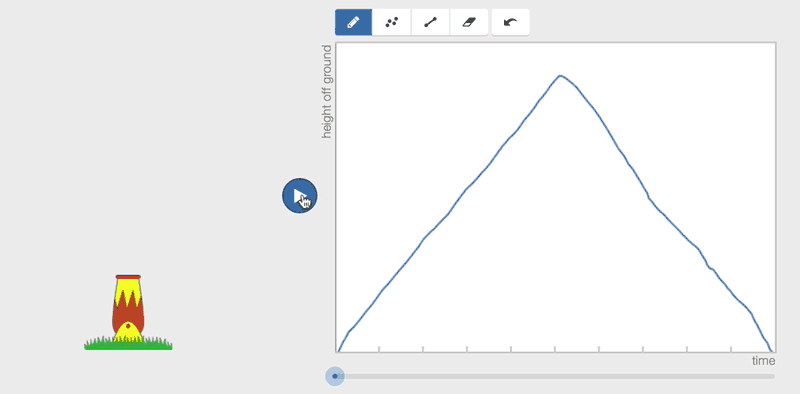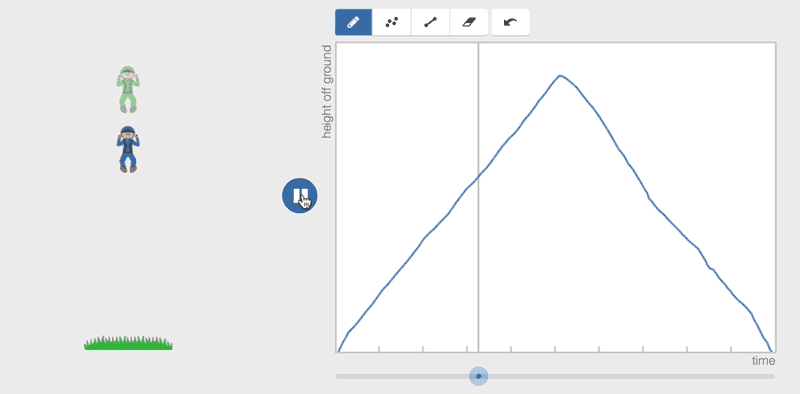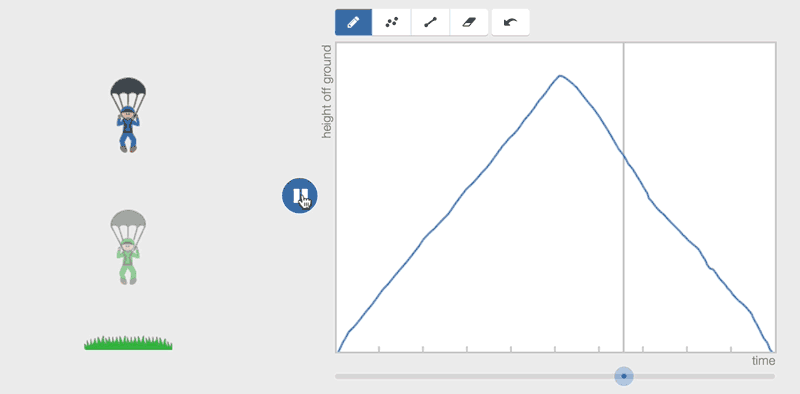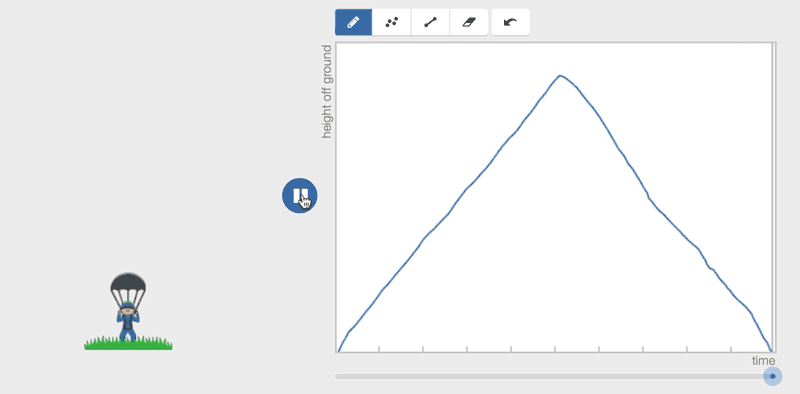
At some point the laptop touch pad made the line weird and it crossed, and all of a sudden there were two little men! Hilarity ensued as we started to move away from the script. She started drawing random lines (some crossing, some starting and stopping) just to see what would happen. 
 
Long story short, we spent the rest of our time (about 30 minutes) trying to make the graph do our bidding in terms of making the little guy move the way we want him too, and choreographing two, sometimes three guys at a time. (And, honestly, hundreds of him at times).

It was truly DE-lightful. 

And, even better, it's apparent she learned something.  I did my own version where I drew little bumps hopping across the bottom third of the graph.  Then I did one where the guy went up really fast and then tried to have his jumps be lower and lower. 

Frankly, my work was not subtle or effective. My girl took over the reigns, made some adjustments to my model and produced something truly sophisticated -- height, time, and speed merged to create a lovely, smooth choreography of bouncing Cannon Man who ultimately disappeared for a moment, and then glided back down. And, this is a child who spends very little time in front of the computer.  

So, the perfect tool to think with, yes? Clear goal, but open ended enough to produce unexpected learning. Intuitive and yet helpful in building skills. Accessible/meaningful to students younger and older than the target audience (MS/HS?).  Isn't the point of an "object to think with" that the student will learn how to use and think with the tool rather than simply work 'as instructed'?  It's clear there was a LOT of thinking happening 'round here this afternoon.

Go read more about their reasoning for making it and try it out for yourself!

Beautiful Objects

I've been thinking quite a lot lately about the role of physical objects in math education.  Sometimes called manipulatives or, more generally, tools, I've discovered conflicting opinions and strategies around the use of such objects. In her book Young Children Reinvent Arithmetic, Constance Kamii helpfully sums up some of the issues with which I've been wrestling:

"Manipulatives are thus not useful or useless in themselves. Their utility depends on the relationships children can make..." p25

"Base-10 blocks and Unifix cubes are used on the assumption that they represent or embody the 'ones,' 'tens,' 'hundreds,' and so on. According to Piaget, however, objects, pictures and words do not represent. Representing is an action, and people can represent objects and ideas,but objects, pictures, and words cannot." p31

So, it is not the object itself that holds the math, but rather the process in which the learner uses the tool that creates the meaning.  But, of course, when we use this kind of language we are talking abstractly about hypothetical objects and generalized characteristics of 'the child,' not any specific object or individual learner in particular.

Too much generality and abstraction drives me crazy so imagine how pleasantly surprised I was when this showed up in my mailbox the other day:

What is it? Well...it's an object. And a beautiful one, at that. An object that can be "manipulated" (the triangle comes out and can be turned). A thinking tool. It was designed and created by Christopher Danielson to investigate symmetry and group theory with his college students. Not only are parts of this tool moveable, but it also has the potential to help "facilitate [mathematical] conversations that might otherwise be impossible." (Christopher on Twitter, Jan 17, 2014)
 
What was even better than getting a surprise package in my real life mailbox containing a real life manipulative (not a theoretical one) was my (real) eight year old's interest in and reactions to said object.

She spotted the envelope and said, "Hey! What's that?!" I told her that a math teacher friend of mine had sent me something he made for his students to use. I took it out of the envelope for her to look at.

First thing she noticed was the smell -- lovely, smokey wood smell which we both loved.  She investigated the burned edges, tried to draw with them (sort of like charcoal). This led to a discussion about laser cutters (heat, precision) and the fact Christopher had designed it.

I pointed out the labeled vertices on the triangle, showed her how you can turn it, and mentioned that the labels help us keep track of how far the shape has turned. She immediately took over this process.  

She repeatedly asked if she could take it to school! I asked her, "What would you do with it?"  She said, matter-of-factly: "Play around with the triangle...and discover new galaxies."

Then, she turned the triangle 60° and said, "And make a Jewish star..." Then she put the triangle behind the the opening so it (sort of) made a hexagon.  I asked, "What did you make there?" She said, "A diaper." Ha! 

I hope Christopher's students are just as curious about and enthralled with the "object-ness" of this gorgeous thing as they are with the idea that it helped them talk and think about things that might otherwise be impossible to grasp.  I know that the objects themselves hold no mathematical meaning but watching how intrigued my daughter was with Christopher's gift, I am left thinking about what we miss out on if we consider a tool simply a bridge to the 'real' goal of mental abstraction.  

Beautiful and intriguing objects, I think, have a role in inspiring the whole of us, all our senses, kinetics, and curiosities, not just our minds, to engage in the process of math learning.  An object doesn't necessarily have to be tangible; narrative contexts are highly motivating 'tools' when working with children. As I blend math, dance and basic art making I see over and over again how presenting the object (idea) first pulls my learners in -- they are curious about what this dance is, how they might weave their own wonderful designs using math, what does she mean "growing triangles" and why are these pennies on the table?  

Learning is hard work, but my experience is that students will gladly work hard if they have even a small sense of the direction in which they're headed.

Meaning in the Making

I had a very interesting conversation with my eight year old over math homework this morning revolving around the commutative property.  Interesting because of her thoughts and also interesting that, for the very first time, I backed away from mathematical correctness, and truly listened to what she had to say. It was fascinating.

The homework asked for factors of various two digit numbers. For 24, my kid put 2x12, 1x24 & 24x1.

I said, "Those last two are the same thing, what other factors can you figure out?"

The response was immediate and somewhat intense. She was convinced that 1x24 and 24x1 were different because that is what the teachers said.

I mentioned we had read about the commutative property in Beast Academy 3B but, sweetly, nothing could sway her loyalty to her teachers and her opinion about what she thought they had taught her.

It was at this point I thought back to all the things Christopher Danielson has written about Cognitively Guided Instruction and the wonderful modeling of his Talking Math with Your Kids project. These approaches show the worth of conversation around math with an emphasis on the adult really listening to what the child is thinking.

She continued. "See! One times twenty four is [pointedly counting] one, two, three, four, five, six, seven, eight, nine, ten, eleven, twelve...twenty four.  Twenty four times one is...[pausing, then saying emphatically] twenty four."

I nodded. "Oh, I see what you're thinking. The first way means you have to count by ones 24 times. The second way you just have to say 24 once."

In her mind it's the process of getting to the final answer that makes the two facts different. Never mind that she gets the same answer both ways. Never mind that she knows all about the "twin facts" on multiplication chart. Never mind that we're having fun finding different ways to memorize multiplication facts including sneaky guerrilla tactics. Nope. This is her reality and it's not going to budge by quoting official definitions.

All I said was,"You can put those two facts on the paper, but your teachers may want you to put some others as well."  In the end she found all the factors of 24, but wrote each combination twice (e.g. 6x4 and 4x6).

In the process of writing my new book, tentatively titled Meaning in the Making: The Body Learning Math, I've been doing a lot of reading and thinking about how the processes of doing and learning math are just as important as the product.  In this case, she can easily figure out factors of two digit numbers, but it's by watching her process closely and engaging in conversation about her thinking where we really get a glimpse into what she knows and how she knows it. Specifically, we can see how she is literally making and reasoning out her own meaning of how multiplication facts are combined. 

We only get half of the picture if we look at the final product/answer (double facts). I know how to watch for and identify understanding through the processes of making math and dance at the same time, but now I'm really learning about how it works with numbers, too! Fun stuff.

Teacher Workshops for Everyone!

Come and dance with me!

I've got a couple Math in Your Feet and Math by Design teacher workshops coming up...

Thursday, April 10, 2014
Clowes Memorial Hall, Butler University, Indianapolis, IN (within driving range from IL, KY, MI and OH!)
Three hours of dig-in, hands-on experience with the the core Math in Your Feet lessons. $30 workshop fee. Participants leave with a comprehensive workshop packet, a link to the classroom materials packet, and new understanding of how you can make math and dance at the same time. More info on the workshop here: http://bit.ly/1ackB7h

June 16-18, 2014
Union College, Barbourville, KY (located in SE Kentucky and within driving range of IN, OH, TN, WV, NC, VA and maybe even GA or SC)
Three days of learning how to integrate math and the arts! Four teaching artists will provide a range of math/art combinations for use in the classroom.  I will be providing a comprehensive program that includes three hours of teacher workshops (as described above) with an additional three hours of work with kids. After your workshop with me, you then get a chance to observe and assist me in the student workshops so you can see how it all plays out with real live kids. Awesome.

There are three separate tracks for primary, intermediate, and middle/high school teachers.  Intermediate teachers will focus primarily on the Math in Your Feet program. Primary teachers will experience the full three-hour Math in Your Feet teacher workshop but observe how I adapt those ideas for younger students; I will also incorporate some Math by Design activities during the student workshop.  Middle and high school teachers will experience and then assist with the Math by Design program.

More info on the Union College summer art/math integration institute will be available in early February.  If you are interested, sign up to receive an e-mail update from me when details become available.

Math Memories

While out shopping for Christmas presents I ran across this:

I hadn't thought of this game for years, but it immediately brought back a memory of being twelve, sitting in my kitchen with a guy my mom had hired to help me with math. He and his family lived out in the woods in some groovy, creative, possibly homeschooling way and he had brought Rack-o for me to play with him. To make math fun, I suppose. I would have none of it. At that point my math resistance was at an all time high.

It may have started back in kindergarten with the bumblebee worksheet. In retrospect, I suppose my five year old brain was just not yet ready for one-to-one correspondence. (My own daughter didn't have that until she was at least six.)

Later in kindergarten we went on a walk off school grounds. I walked ON one of the white lines as we crossed the street.  Teacher called out: "Malke! You're supposed to walk BETWEEN the lines!"  I distinctly remember thinking that I thought she said "walk ON the line".  I know for sure I was thinking that I thought I was following directions. On, in, between, under, over, etc. are a huge part of math learning at this age so it makes sense that I might have been confused. I did not like being yelled at.

In fourth grade I noticed my teacher putting up some math papers that had been graded 100%.  Mine was not displayed on the bulletin board despite the fact I had correctly answered every question.  When I asked my teacher why my paper had not been included she replied that it wasn't neat enough. I shocked.  Yes my paper was full of smudges and eraser marks, but I took that as evidence of my hard work and determination. I didn't challenge my teacher about it, but to this day I always look for ways to admire children's efforts as well as their final product.

Fifth grade math class. Timed math facts test. I was in the front row. In the middle of the test, my (male) teacher bellowed at me: "NO FINGERS." First five or six students to complete the test got to play with the OWL CALCULATORS. They were all boys. I am still bitter.

High school. 11th grade? Asked guidance counselor to be transferred from Mr. X's algebra class to Mr. Y's.  I told her, I just want to learn the math. Mr. X just sits there and talks the whole class -- I want Mr. Y because I know I can learn from him. Counselor says, I know, I understand, but I just can't. That was the year I helped Shelly Heesacker study for a math test. She got an A. I got a C.

Not developmentally ready. Product valued over process. Timed tests. "Teaching" by talking. These are not tragic circumstances, by any means, and are not meant to malign math education as a whole, but it's interesting that these math memories are still with me, so many years later.

In with the New!

Hey ho! 2013 is so...yesterday! I'm celebrating a sparkly new year with a new website! Take a minute to check it out and let me know how I can help you or your students learn and make math in new ways in 2014. www.malkerosenfeld.com