The Math in Your Feet Blog | Constructing an Understanding of Mathematics
Monday, March 31, 2014
Saturday, March 29, 2014
Grid Art, Patterns & #tmwyk
Math related conversations with my 8 year old tend to pop up unexpectedly. These are often around something she's making, and are often a gorgeous little gem of a surprise. Today was no different.
I found her creating a grid of tape on top of a piece of origami paper. She was coloring it in when she said, "You know, mama, patterns don't necessarily have to be colors in order."
Oh my gosh!
Me: What do you mean by that?
As you can see from the picture, below, she was coloring the whole page somewhat randomly, sometimes following the columns down, sometimes not.
Her: Well, the colors don't have to be regular, they just need to be in the windows."
Me: You mean the windows are the places where the tape is not covering the paper, that's what you're looking at? It doesn't matter what color windows are, just that they're colored in?
Her: Yeah.
So here I pause to do a happy dance. My biggest discontent around patterns is that many kids grow into adults who think that "patterns" are only linear repetitions of colors. It is clear she has not internalized that particular reality. The other reason I'm happy is that Prof. Triangleman once said to me:
This really goes to show you that it's worthwhile to keep your ears open while kid is focused on making or building something. Even if it's after the fact, ask your kids to tell you about what they did, even if it doesn't look like much. I mean, just look at the taped/colored piece again. It's pretty much a bunch of scribbles and it'd be super easy to pass it over, to think it was nothing special. In reality, though, there was so much thinking going on while she worked.
Here's what the piece looked like when she took the tape off:
Her: Oh.
Me: You seem surprised. Did that not turn out the way you expected?
Her: Why do you sound like a journalist?
I found her creating a grid of tape on top of a piece of origami paper. She was coloring it in when she said, "You know, mama, patterns don't necessarily have to be colors in order."
Oh my gosh!
Me: What do you mean by that?
Me: You mean the windows are the places where the tape is not covering the paper, that's what you're looking at? It doesn't matter what color windows are, just that they're colored in?
Her: Yeah.
So here I pause to do a happy dance. My biggest discontent around patterns is that many kids grow into adults who think that "patterns" are only linear repetitions of colors. It is clear she has not internalized that particular reality. The other reason I'm happy is that Prof. Triangleman once said to me:
"Math is when you say exactly what it is you want to pay attention to, focus only on that attribute and ignore everything else."She was doing this! Her pattern has 'windows' that are colored in, but the pattern is not defined by the colors themselves. She was consciously creating a pattern of windows (spaces between!) and consciously excluding the colors. I am thrilled to have caught a glimpse of this multi-layered attention in action.
This really goes to show you that it's worthwhile to keep your ears open while kid is focused on making or building something. Even if it's after the fact, ask your kids to tell you about what they did, even if it doesn't look like much. I mean, just look at the taped/colored piece again. It's pretty much a bunch of scribbles and it'd be super easy to pass it over, to think it was nothing special. In reality, though, there was so much thinking going on while she worked.
Here's what the piece looked like when she took the tape off:
Me: You seem surprised. Did that not turn out the way you expected?
Her: Why do you sound like a journalist?
Monday, March 24, 2014
Saturday, March 22, 2014
Step Dance Saturday: The Warner Sisters & KIDS! (Video)
Hello and welcome to what will likely be a sporadic series called Step Dance Saturday! Our inaugural video is of one of my favorite step dancers, Melody Cameron, her sister, and a few of her sister's kids! They live and dance on Cape Breton Island, which is part of Nova Scotia, Canada.
The dancing starts in the traditional way, with a Strathspey which transitions to a reel. The Melody and her sister have choreographed their steps for this part.
When the two girls come on stage, they position themselves for the reel portion of the Scotch Four, a very old figure dance. Both the figure and the step dancing itself originated in Scotland. From this point in the video all the dancing is improvised, each dancer putting steps to the music as they wish.
As you watch, you can look for patterns of footwork performed on one side of the body and then repeated on the other side. It may take more than one viewing to be able to see those patterns. If you want an added challenge, see if you can figure out the pathways the dancers are taking during the Scotch Four!
Happy Dancing!
The dancing starts in the traditional way, with a Strathspey which transitions to a reel. The Melody and her sister have choreographed their steps for this part.
When the two girls come on stage, they position themselves for the reel portion of the Scotch Four, a very old figure dance. Both the figure and the step dancing itself originated in Scotland. From this point in the video all the dancing is improvised, each dancer putting steps to the music as they wish.
As you watch, you can look for patterns of footwork performed on one side of the body and then repeated on the other side. It may take more than one viewing to be able to see those patterns. If you want an added challenge, see if you can figure out the pathways the dancers are taking during the Scotch Four!
Happy Dancing!
Sunday, March 16, 2014
3 Ways to Bring Math in Your Feet to Your Area
Would you like me to come to your area to share the Math in Your Feet and/or Math by Design programs? Are you interested in a professional learning opportunity or a homeschool event? Not sure how to get that to happen? Wonder no more...here are three ideas to make my visit to your locale a reality!
Find a Presenting Organization
Look around your area and see if there are any performing arts venues, children's museums, or math and science museums with education departments that present children's performances and/or teacher workshops throughout the year. This is a particularly good option if you and your friends and colleagues are a mix of school- and home-based educators. Once you've identified a possible venue, let me know and I'll be happy to make contact, unless you'd like to take that step. If that's the case, you can point folks toward malkerosenfeld.com or mathinyourfeet.com to look at videos and other information about the workshops.
Find a School or School District
Do you have district- or school-wide professional development days? Would you value an option for active participation and learning that goes deep into the hows and whys of merging math and movement that also connects to necessary CCSS for Mathematics AND gives you specific experience with a road-tested program (not to mention all the materials you need for classroom implementation)? Feel free to e-mail the appropriate administrator to suggest Math in Your Feet! You can point them to mathinyourfeet.com or malkerosenfeld.com to find short videos of my work, publications, and workshop descriptions.
Go Rogue
Email me if you're interested in how to set up an event yourself! This option would likely include tasks such as securing a space, getting the word out, and insuring a minimum number of participants to share the costs of my fee and travel expenses. It's also the perfect option for homeschooling networks -- including the possibility of kids & adults learning together!
Logistics: Cost generally include a fee, travel (air or mileage) and lodging, if needed. I'm happy to talk pricing details via phone call or e-mail.
Find a Presenting Organization
Look around your area and see if there are any performing arts venues, children's museums, or math and science museums with education departments that present children's performances and/or teacher workshops throughout the year. This is a particularly good option if you and your friends and colleagues are a mix of school- and home-based educators. Once you've identified a possible venue, let me know and I'll be happy to make contact, unless you'd like to take that step. If that's the case, you can point folks toward malkerosenfeld.com or mathinyourfeet.com to look at videos and other information about the workshops.
Find a School or School District
Do you have district- or school-wide professional development days? Would you value an option for active participation and learning that goes deep into the hows and whys of merging math and movement that also connects to necessary CCSS for Mathematics AND gives you specific experience with a road-tested program (not to mention all the materials you need for classroom implementation)? Feel free to e-mail the appropriate administrator to suggest Math in Your Feet! You can point them to mathinyourfeet.com or malkerosenfeld.com to find short videos of my work, publications, and workshop descriptions.
Go Rogue
Email me if you're interested in how to set up an event yourself! This option would likely include tasks such as securing a space, getting the word out, and insuring a minimum number of participants to share the costs of my fee and travel expenses. It's also the perfect option for homeschooling networks -- including the possibility of kids & adults learning together!
Logistics: Cost generally include a fee, travel (air or mileage) and lodging, if needed. I'm happy to talk pricing details via phone call or e-mail.
Sunday, March 9, 2014
A Few Thoughts on "Concreteness"
In the past week or so I've had run-ins with very specific views on concrete-ness and abstract-ness. There are many people who feel very strongly about the notion that concrete objects create a bridge to more abstract ideas especially for young children. And, even if the discussions sound different, this viewpoint is not reserved exclusively for the little ones.
In any case, I used to be a strong believer in the concrete-to-abstract continuum but the more I read the more convinced I am of the pedagogical dangers that arise by taking this progression too literally. I also get the sense that 'abstract' in the context of these kinds of discussions is sort of code for 'hard to understand'.
This post is not intended to discuss or argue these points in full, only to share some thoughts I've run across in the last few months in order to illustrate why this topic is not as straightforward as some might believe.
First, from Uri Wilensky, a seriously brilliant take-down of the whole issue in his 1991 article Abstract Meditations of the Concrete and Concrete Implications for Mathematics Education. Here are just a few excerpts. I recommend reading the whole thing to fully understand his points.
At the same time, she points to the reality that "children learn easily and joyfully from real things":
And this is the conundrum in which we find ourselves, isn't it? Physical objects not only create sensory memories but also help mediate what's in our minds to expression through our bodies. However, it seems that things are further complicated: Our bodies are strong, capable and skilled but, for some reason which is fully outside my area of expertise, it seems that our physical selves require augmentation in order to fully realize and express our individual and collective visions. I think that's why it makes sense to think that physical objects could be an effective mediator in math learning, especially when math appears to be an extremely abstract subject...
...and now we are full circle, back again to Uri Wilensky, who said:
It's nice to have some of this thinking out of my head for now. Any thoughts?
In any case, I used to be a strong believer in the concrete-to-abstract continuum but the more I read the more convinced I am of the pedagogical dangers that arise by taking this progression too literally. I also get the sense that 'abstract' in the context of these kinds of discussions is sort of code for 'hard to understand'.
This post is not intended to discuss or argue these points in full, only to share some thoughts I've run across in the last few months in order to illustrate why this topic is not as straightforward as some might believe.
First, from Uri Wilensky, a seriously brilliant take-down of the whole issue in his 1991 article Abstract Meditations of the Concrete and Concrete Implications for Mathematics Education. Here are just a few excerpts. I recommend reading the whole thing to fully understand his points.
Second, in all my reading there is a theme of caution: the adult can see the math in the materials but this may not be evident to the child. Piaget himself cautioned that the materials themselves cannot and do not hold mathematical meaning. As Kamii says in Children Reinvent Arithmetic (2nd Edition):"If we adopt the standard view [of concrete], then it is natural for us to want our children to move away from the confining world of the concrete, where they can only learn things about relatively few objects, to the more expansive world of the abstract, where what they learn will apply widely and generally.
"Yet somehow our attempts at teaching abstractly leave our expectations unfulfilled. The more abstract our teaching in the school, the more alienated and bored are our students, and far from being able to apply their knowledge generally across domains, their knowledge displays a "brittle" character, usable only in the exact contexts in which it was learned ...
"...I now offer a new perspective from which to expand our understanding of the concrete. The more connections we make between an object and other objects [not always physical, could mean ideas], the more concrete it becomes for us. The richer the set of representations of the object [idea], the more ways we have of interacting with it, the more concrete it is for us. Concreteness, then, is that property which measures the degree of our relatedness to the object, (the richness of our representations, interactions, connections with the object), how close we are to it, or, if you will, the quality of our relationship with the object."
"Base-10 blocks and Unifix cubes are used on the assumption that they represent or embody the 'ones,' 'tens,' 'hundreds,' and so on. According to Piaget, however, objects, pictures and words do not represent. Representing is an action, and people can represent objects and ideas, but objects, pictures, and words cannot." p31In the introduction to Mathematics Their Way by Mary Baratta-Lorton (a classic activity-based math curriculum for K-2 first published in 1976) the author provides an interesting take on this idea:
At the same time, she points to the reality that "children learn easily and joyfully from real things":
And this is the conundrum in which we find ourselves, isn't it? Physical objects not only create sensory memories but also help mediate what's in our minds to expression through our bodies. However, it seems that things are further complicated: Our bodies are strong, capable and skilled but, for some reason which is fully outside my area of expertise, it seems that our physical selves require augmentation in order to fully realize and express our individual and collective visions. I think that's why it makes sense to think that physical objects could be an effective mediator in math learning, especially when math appears to be an extremely abstract subject...
...and now we are full circle, back again to Uri Wilensky, who said:
In other words, it is the process of building multiple and varied relationships with an idea that makes something 'concrete' to the learner, not the properties of the physical objects themselves."...any object/concept can be become concrete for someone. The pivotal point on which the determination of concreteness turns is not some intensive examination of the object, but rather an examination of the modes of interaction and the models which the person uses to understand the object. This view will lead us to allow objects not mediated by the senses, objects which are usually considered abstract - such as mathematical objects - to be concrete; provided that we have multiple modes of engagement with them and a sufficiently rich collection of models to represent them."
It's nice to have some of this thinking out of my head for now. Any thoughts?
Tuesday, March 4, 2014
From My Feeds to Yours: Six Interesting Things
I don't think I've ever done a post like this before but, then again, I don't think I've run across so many wonderful, thoughtful, helpful blog posts in such a short time. In other words, there's been a plethora of fabulous thinking and writing showing up in my feeds, all of it related to math education in some way.
Here's what has inspired me in the last week or so:
From Michael Jacobs in Canada comes some really interesting thinking about connecting spatial skill development to math class in intentional ways. He alerted me to the fact that my Mathagogy video was being shown at a meeting focusing on this topic. This chance reminder about spatial reasoning reminded me that as a dancer teaching math and dance and writing a book about math and dance I really want and need to understand this topic more deeply. All this got me thinking. I love it when that happens. Here's Michael's post on spatial reasoning.
----------------
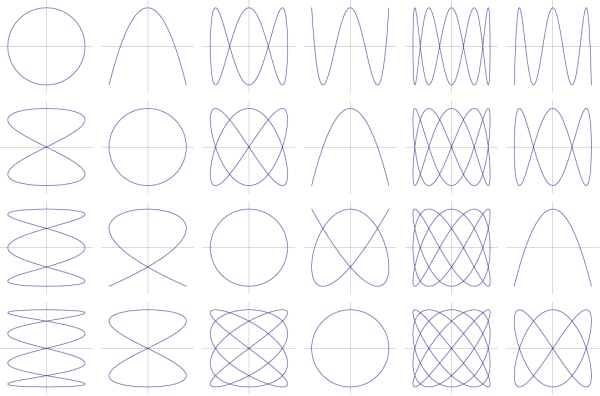
Another chance encounter on Twitter was with Edmund Harriss and his post Rational Parameterisation of the Circle. The images above are Lissajous curves and they made me wonder how they might be used as interesting choreographic prompts; I immediately started wondering how to turn all that math into a meaningful math/dance inquiry in the classroom. Our conversation helped me realize that it might actually be a really cool project. Hopefully we'll be able to work out some more ideas about this while at Twitter Math Camp in July.
----------------
Then there was a lovely, detailed article in The Atlantic blog featuring an interview with Maria Droujkova about her vision for helping young children and their parents make math meaningful in their own lives.
----------------
This week there was also an excellent piece from Edward Frenkel, How our 1,000 year old math curriculum cheats America's kids. Read it together with Maria's interview piece and the two together really pack a wallop in terms of creating a beautiful big picture of how important it is to include the exciting big ideas in math learning.
Here's what has inspired me in the last week or so:
From Michael Jacobs in Canada comes some really interesting thinking about connecting spatial skill development to math class in intentional ways. He alerted me to the fact that my Mathagogy video was being shown at a meeting focusing on this topic. This chance reminder about spatial reasoning reminded me that as a dancer teaching math and dance and writing a book about math and dance I really want and need to understand this topic more deeply. All this got me thinking. I love it when that happens. Here's Michael's post on spatial reasoning.
----------------

Another chance encounter on Twitter was with Edmund Harriss and his post Rational Parameterisation of the Circle. The images above are Lissajous curves and they made me wonder how they might be used as interesting choreographic prompts; I immediately started wondering how to turn all that math into a meaningful math/dance inquiry in the classroom. Our conversation helped me realize that it might actually be a really cool project. Hopefully we'll be able to work out some more ideas about this while at Twitter Math Camp in July.
----------------
I happened upon the curves post just after doing a little math/dance investigation in my own dance style this morning. I typed up a little report and posted it to the Math in Your Feet Facebook page. Here's part:
"Today's little dance/math tidbit, an odd over even experiment ...Ultimately, I can only do the 13 beat phrase twice w/out naturally trying to even things out, partly because the music & dance work together so closely. Putting the dance 'at odds' with the music can have some really cool results, but in the case of this experiment I may need to dial it back a little."----------------
Then there was a lovely, detailed article in The Atlantic blog featuring an interview with Maria Droujkova about her vision for helping young children and their parents make math meaningful in their own lives.
“You can take any branch of mathematics and find things that are both complex and easy in it,” Droujkova says. “My quest, with several colleagues around the world, is to take the treasure of mathematics and find the accessible ways into all of it.”I have gained so much from interacting with Maria through her Natural Math and Moebius Noodles projects, and am honored to be included as a contributing blogger on the Moebius Noodles site and also asked to co-author a book with her Delta Stream Media company. Keep your eyes out for Socks are Like Pants, Cats are Like Dogs a book of games, puzzles and making activities around the ideas of variables, attributes, sorting and more which I am co-authoring with Gord Hamilton of Math Pickle. Our manuscript is almost complete!
----------------
This week there was also an excellent piece from Edward Frenkel, How our 1,000 year old math curriculum cheats America's kids. Read it together with Maria's interview piece and the two together really pack a wallop in terms of creating a beautiful big picture of how important it is to include the exciting big ideas in math learning.
----------------
If you work in a classroom, this post from Fawn Nguyen on Classroom Management is full of wisdom:
If you work in a classroom, this post from Fawn Nguyen on Classroom Management is full of wisdom:
"We can't say we possess great classroom management skills if we could pick and choose where and whom to teach. There's a quote out there that I like: Parents are sending us their best; they're not keeping the good ones at home. So, if we took the students out of the classroom-management-success equation, we are left with two variables: the teacher and the classroom."
And there you have it. A whole lot of what's interesting to me, just for you!
Sunday, March 2, 2014
My Daughter the Map Maker [Spatial Reasoning]
I'm thinking about spatial reasoning: what it is, how its developed, and how it interacts with math learning. Also, why it is not spoken of much in my Twitter feed which happens to be a veritable goldmine of priceless thinking and information related to math education.
Yesterday, my 8yo and I went to the KidsCommons, a children's museum in Columbus, IN well known for it's larger-than-life toilet which resides inside an otherwise kid-scaled house. You climb in, there's a flushing sound, and then there's a slide to the bottom floor of the house.
This morning my kid woke up and immediately started describing all the little hidden passages inside that three-storied play house the adults can't really access. Then she said: "I'm going to draw you a map!"

So she did and, when finished, talked me through what she had drawn. Observing all this I was reminded, yet again, that she has been expressing her ideas through maps for as long as I can remember.
Drawing and reading maps is a key spatial reasoning skill.
This one is from our house to Grandma's house in Ohio, drawn one morning when she was newly six:

Half a year later, she was still drawing lots of maps. In this one she mapped out a set of sequential instructions for sewing a dress:

We've made and played games with maps (this one is about capturing territory for our kitty clans):

There was her "map of angles"

And the time that she and her friends found a real x-marks-the-spot treasure map (on birch bark, no less) at the Farmers Market and spent 30 minutes investigating where that X was in real life. They found it.

Here's just one more map, where I wrote:

Later on in that post (written over 1 1/2 years ago) I write:
There's lots of information out there about tests for determining spatial reasoning skills, many of them very specifically about rotating 2D and 3D shapes in one's mind. It also appears, based on some cursory reading, that one can improve one's spatial reasoning skills using activities that are similar to these tests.
But there seems to be precious little documentation related to the intentional pedagogy of and reasoning around the development of spatial skills.
Does the development of spatial reasoning and math reasoning interact? If so, how do we gracefully fold spatial skills into the daily mathematical lives of our students? I have a feeling doing so could be very fun, as well as beneficial.
In a sense, these map artifacts from my daughter's life over the past 2+ years have become a treasure map of sorts for me as I try to figure this out. I always love company on my journeys -- if you have any insights, personal experiences, or aha! moments about what it looks and sounds like to include spatial reasoning in the classroom in an intentional way, please do get in touch.
Yesterday, my 8yo and I went to the KidsCommons, a children's museum in Columbus, IN well known for it's larger-than-life toilet which resides inside an otherwise kid-scaled house. You climb in, there's a flushing sound, and then there's a slide to the bottom floor of the house.
This morning my kid woke up and immediately started describing all the little hidden passages inside that three-storied play house the adults can't really access. Then she said: "I'm going to draw you a map!"

So she did and, when finished, talked me through what she had drawn. Observing all this I was reminded, yet again, that she has been expressing her ideas through maps for as long as I can remember.
Drawing and reading maps is a key spatial reasoning skill.
This one is from our house to Grandma's house in Ohio, drawn one morning when she was newly six:

Half a year later, she was still drawing lots of maps. In this one she mapped out a set of sequential instructions for sewing a dress:

We've made and played games with maps (this one is about capturing territory for our kitty clans):

There was her "map of angles"

And the time that she and her friends found a real x-marks-the-spot treasure map (on birch bark, no less) at the Farmers Market and spent 30 minutes investigating where that X was in real life. They found it.

Here's just one more map, where I wrote:
"She used the new graph paper I had printed out for our graphing game and as she drew she described to me how each color, line and picture symbolized a landmark along our [walking] route downtown. She even threw in a fractal tree to represent the campus woods."

Later on in that post (written over 1 1/2 years ago) I write:
"She seems really drawn to visual representation as a way to communicate to others what she knows, especially math concepts. Over the last year she has shown me what she thinks and understands through spontaneous, unprompted creation of charts, maps, and diagrams; often these are private ruminations that I happen to unearth while tidying up after bedtime. I view these self-initiated efforts to symbolize and quantify (in a way that makes sense to her) as a kind of bridge between the experience and her eventual use of standard mathematical notation and representation.This is a particularly important to thing to re-read as it has led me to a very interesting realization: I have always assumed spatial concepts as being part of mathematics. But, maybe they're not?
There's lots of information out there about tests for determining spatial reasoning skills, many of them very specifically about rotating 2D and 3D shapes in one's mind. It also appears, based on some cursory reading, that one can improve one's spatial reasoning skills using activities that are similar to these tests.
But there seems to be precious little documentation related to the intentional pedagogy of and reasoning around the development of spatial skills.
Does the development of spatial reasoning and math reasoning interact? If so, how do we gracefully fold spatial skills into the daily mathematical lives of our students? I have a feeling doing so could be very fun, as well as beneficial.
In a sense, these map artifacts from my daughter's life over the past 2+ years have become a treasure map of sorts for me as I try to figure this out. I always love company on my journeys -- if you have any insights, personal experiences, or aha! moments about what it looks and sounds like to include spatial reasoning in the classroom in an intentional way, please do get in touch.
Subscribe to:
Comments (Atom)






