Moving Forward: The New 'Making Math' Page!

So, you may or may not have noticed that this is a multi-topic blog. 

I am a teaching artist who finds connections between math and percussive dance.  I give kids the tools to explore space and time.  I give their teachers the tools to bring body-based inquiry into their own classrooms.  I started this blog to share my thoughts and ideas on creative (as in creating something), hands-on, hopefully kinesthetic learning, wherever it may happen. 

This blog also documents my inquiry into what it means to 'do' math.  I've been lucky enough to connect with a bunch of really smart people in the math ed world who have helped me toward my goal.  When I first started the blog I had a hunch that there was more math embedded into the dance work we do in my program Math in Your Feet. I wanted to figure out what it was and how to explain it. 

Sixteen months in, I finally feel like I've made some real progress!  You can read about my big aha! moment about attributes here.  You can also read about the moment when I uncovered an important connection between my art form and making meaning in mathematics, both of which incoporate moving patterns.  It's probably my all-time favorite post.  So far.

There is no way of anticipating how far I will go on this journey but recently I've begun to feel like I'm reaching another bend in the river.  I am more fascinated than ever with what it means to think mathematically and how that skill is developed, especially in preschool and elementary age children.  And, I'm a mom of a snappy six year old who accuses me of being a 'math mommy!' because, well, I am.  I find inspiration in her learning, and within that process I find some of the answers I've been searching for.

In the last two months I've noticed a trend in my post topics.  Nearly all of them outline some kind of hands-on project that has helped me, or my kid, or both of us, deepen our understanding of math.  Not all of these activities are original, but every 'making math' post is a snapshot of our inquiry.  Some of these activities were born out of some inspiration or question, but they are all easy to reproduce on your own and deliciously open ended (no wrong answers!).   I've decided to put them in their own section in the hopes you might find them useful in expanding or deepening your own understanding of math.  I plan to add to this collection over time.

I invite you to take a look at the new Making Math page and see if there's something you'd like to do with your students or kids.  Most, if not all, of these projects can be easily done in some way by the youngers (usually with adult support) but also fully enjoyed by the olders, both in school and out.  As Maria Droujkova of Natural Math and Moebius Noodles says: "'Make your own' is such a simple and powerful way to open mathematical depth. Like a game? Make your own!"

Make Your Own Attributes Matching Game!

I have had attributes on the brain for a couple weeks now.  Most of my thinking has been on how the practice of identifying similarities and differences (a closed process) really opens up when put into a design context. 

So, given how much I've been thinking about it, it's no wonder that what I thought would be a ho-hum, pass the afternoon kind of game turned into an incredible brainstorm. 

The kid and I were playing a Blue's Clues matching game.  I was, truth be told, not 100% engaged, but it was a pleasant enough way to pass some time.  At some point I noticed that this particular matching game was really quite tricky.  You'd turn over two cards with green dogs on them but they were different in some very tiny ways. 

Despite some very minor irritation that I might actually have to pay attention, I started to think about what those game designers were doing.  Nothing like a little internal meta-conversation to help put the pieces together....

Click!

Attributes!  On the matching game (brilliant, brilliant, game designers)!  What if we made our own?  Could we make our own?

"Do you wanna make our own matching game?" I asked the kid.  

Needless to say, the answer was yes.  We rushed around the house trying to locate the 3"x5" cards but, of course, they were nowhere to be found.  I rounded up some other paper, the paper cutter, some shapes to trace, and the crayon caddy. 

It was fast and furious, but in the midst of it all we managed to agree on my some parameters:

Geometric shapes only. This is (sneaky) math after all.  We used tangram pieces, pattern blocks, some Cuisenaire rods, and some magnets from the fridge.

Each pair of cards has to be exactly the same.  It's never too early to experience congruence, and what better way to do that then to be personally responsible for it?  This is a key point in my still-developing argument (one that is based on my experience with Math in Your Feet as well as what I've been doing lately) -- it's one thing to observe congruence, it's another to have to be congruent yourself.  I realized as we went along that the 'make a game' energy really motivated my kid to do this part up right. She paid a lot of attention to sameness in her designs.

Each pair of cards have to be different from the other sets in some way.   We have yet to explore this fully, but this means that if you make make more than one set of triangle cards, the sets have to be different from each other in color or design or size.

It's this last point that created the most conversation as we created our cards together.  According to the kid, I was altogether too boring in my designs.  I would say, "But every design you make is colored in!  They have to be different from each other, so I'm going to leave mine uncolored."  This, apparently, motivated her to copy my 'boring' designs and make them 'more interesting' than mine!

So, we had a lot of levels of similar and different going on, including not only what we created but how we were doing it and what our personal design aesthetic was and how these creative choices were different or similar from each other.  My brain hurts just thinking about it!  See what you think:





All told, and in very short order, our prototype set of matching cards totalled fourteen pairs, which made for a very satisfactory game.  I'd love to find a calmer time to for us to work more slowly, carefully, and thoughtfully on another set.  She wants to make sets of matching games to sell at her ever-evolving lemonade-origami-bookmark stand in the spring, which I think might be motivation enough to take a closer look at how to generate similarity and differences. 

If you end up making your own attribute matching game I would SO love to see what you create (please, please, please?!?).

Take Your Kid to Work Day

In this case it was "take your kid to 'help' set up the space" day.  For me, every new space presents its own unique set of challenges and it's nice to be able to set it up ahead of time.  That way I don't have to drive 60 to 90 minutes, set up a new room, teach five classes of kids I've never met before, and drive home, all on the first day of a residency. 

Here's what part of this one will look like on the first day (I was way too busy problem solving to take lots of pictures and, anyway, it's really a boring space without the kids):

Here's my dance board plus the student spaces for demonstrating to the class.  Notice the carpet.  In this case we have enough space, but the kids won't be able to hear the sounds their feet make.  But that's okay, we'll still be doing awesome work.

 Here's my kid on 'take your kid to work' day.  She helped me put up the posters, move some chairs and then decided to play with tape.  Lucky kid.  I don't have pictures, but she made two really long lines of tape so she could do cartwheels down one and roll tape rolls down the other. 

When I was helping her put the tape down I casually mentioned that we need to make them parallel so that they'd be the same distance apart all the way up and down the line.  After that she took a closer look at the Turns poster (see first picture) and went over to the table to make a poster for her own dance and math class.

Translated into standard English, it reads:  "Cat Dance. Cat Math.  Phone Number.  GO.  Choreography.  Performing Cats."  Sounds fun!

You also might notice the effect the environment and conversation had on her illustrations.  I especially like the square with arrows radiating out of it in all directions (probably influenced by the Turns poster).  And, in the illustration of shapes, along with the circle, triangle and square are a set of parallel lines! 

[A side note: Her spelling is making noticeable gains in the past week.  I have to say that's a pretty good go at 'choreography' and 'performing' for a kid who, as recently as last week, skipped all the vowels when sounding out her words, lol!  Isn't brain development spooky?]

She figures that six participants will be enough for the class to run.  If you sign up she'll send you more information in the brochure she made on the car ride home.

Let's Play "How Much Change is in Mama's Purse!?"

I was going through the Common Core State Standards for Mathematics the other day, to finalize a document that illustrates the connections between the CCSS and my program Math in Your Feet.  I was really focusing on fourth and fifth grade standards, but while I was there I peeked in on the first grade standards as well.  I was curious.

I've got a first grader of my own, and I shepherd her math learning.  I watch her figure out how numbers work and relate to each other and I observe her make observations and formulate questions while experimenting with shapes and other manipulatives.  So, I really liked looking at the CCSS to put all that work into perspective.  The content standards were all pretty straightforward but I immediately started trying to figure out how I could really know if those words meant things my kid knows.   What does her understanding look like in action? 

Luckily for me, it turns out that a great way to assess a lot of what a first grader knows and can do, mathematically speaking, is to look inside my purse!

We were having a late lunch/early dinner at our local co-op.  The plan was to eat a nice balanced meal and then hit the bulk bins for chocolate coconut candies after that.  I was digging around in my purse to make sure I had enough money to get the promised after-dinner treats.

Digging...digging...and finally finding a handful of coins.  That's when inspiration struck.

"Hey!  Let's figure out if I have enough to buy dessert!"

Unfortunately my camera was at home with battery charging, but the following photos are a faithful re-creation of the independent thinking that followed.

Showing no hesitation she went for the quarters first.  Lined them up, counting by 25, dollar by dollar.  Got the dimes in line counting by ten, and finished out that dollar with nickles (by 5's) and pennies (by 1's).  Added it all up in her head, no fingers (you go, girl!).  The grand total? $5.07.

"Which coins make the highest stack?" I wondered.

We made stacks from tallest to shortest, quarters, pennies, dimes and nickles.  And then I remembered attributes, and we compared each coin and ordered them thick to thin.  Turns out the phrase 'one thin dime' could also almost be 'one thin penny' by a hair.  You'll also notice that putting them thickest to thinnest lines them up biggest coin to smallest coin.  Hmmm...I wonder how that happened?

What did all this dinnertime inquiry show me about my daughter's math skills in relation to the CCSS? 

First, it's important to remember that using money is just one of many ways to represent numbers and understanding of numerical relationships.  As an instructional tool, I think that using money is one of the best ways to develop numeracy. You're working with a whole unit of 100, for one thing, and anything less is a fraction of the whole.  Also, the random sizes -- a dime is worth more but smaller than a nickel -- is a fabulous conceptual challenge, and think of all the different kinds of skip counting!  Plus, money amounts are always changing depending on what you save, spend, or find on the ground, so there's always something new to figure out.

So, she can represent her numerical understanding through money and mental calculations, but although she likes to write out simple equations, we haven't done much with adding larger numbers on paper.  After reading Peggy Kaye and Constance Kamii (which I've written about here and here), I'm fine with it that way for now. 

As for the standards, most of 'how much money in the purse' challenge was related to numeracy skills but, overall, the activity showed me that my daughter is gaining mastery in multiple content ares in three of the four content domains:

Operations & Algebraic Thinking: "Developing understanding of addition, subtraction, and strategies for addition and subtraction within 20."
Numbers & Operations in Base Ten: "Developing understanding of whole number relationships and place value, including grouping in tens and ones."
Geometry: "Reasoning about attributes of, and composing and decomposing geometric shapes."

The other half of the CCSS for math is the Mathematical Practices section. The change in my purse also illustrated these goals in action at the first grade level:

"...adaptive reasoning, strategic competence, conceptual understanding (comprehension of mathematical concepts, operations and relations), procedural fluency (skill in carrying out procedures flexibly, accurately, efficiently and appropriately), and productive disposition (habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy)."

In this case the mathematics was most certainly 'sensible, useful and worthwhile'!  Although the change in my purse did not asses everything in the practices section, of course, it was helpful to have a spontaneous moment to see up close not just what she knows but how she goes about using what she knows.  On the whole, I feel confident things are going in the right direction.

And, in case you're wondering, the chocolate coconut clusters were delicious!

You Can't Plan Perfect

I l.o.v.e. when things fall seamlessly into place. 

We've been talking about pentominoes for a week.  This morning I had the thought that today would be the perfect day to find some.

Looking for audio books at the library, we run across Chasing Vermeer by Blue Balliett. 

I say: "Hey, here's that book I was talking about. The boy carries a set of pentominoes in his pocket and uses them to solve a mystery about a missing piece of art. Wanna get it?"

We drive to the other side of town and find a beautiful set of lemon yellow overhead pentominoes for $4.

The kid can't wait and opens the pentaminoes bag in the car.  Plays with them.  Starts singing..."Is-o-be-ell...lo-o-o-ves...pen-ta-mi-noes!"

We're home and the kids pulls out the pentominoes and starts the book.  I'm typing 'how to use pentominoes' into Google and the narrator starts to read..."About pentominoes..."

A few minutes later, the character Calder has just finished making a rectangle using seven pentominoe pieces and I look over and the kid has a rectangle in front of her.  I go over quickly and count her pieces...eight! 

You can never plan for something this wonderful. 

Mapping the Familiar

There was a bright, blue sky up above, and at ground level there was frozen fog.  The result was a morning delicately dressed in sparkles.  Perfect for a walk.

Down the driveway.  Pick a piece of lavender, covered with millions of tiny ice crystals.  Which way do you want to turn, left or right?  Next intersection, right or left? 

We walked through the fog, already burning off.  We could feel the sparkles entering our lungs with each breath.

Busy road and cars zooming.  Three choices, right, left, or straight ahead.  "Mama, I used to be afraid of those trees, but I'm not any more."  We pick tiny pine cones off the tips of the branches. 

Next crossroads, "Mama, that's University Street down there, let's go there."  Thinly frozen puddles alongside thinly disguised reading practice: "What does that P stand for, do you think?  The one with the red circle and the cross over it?  What does the rest of the sign say?" I ask.

Right turn down University and an old dog barking at us across the lawn.  "Mama, I used to be afraid of dogs, but now I just don't like their licking."

Find two sticks, clap them together and then we're marching.  Left turn.  Right turn. Rose street!  Find the stone pig, march on home.  "I wanna make a map!" the girl says.

She wanted red and blue like the roads in the atlas.  We recalled which way we turned, what we saw, remembered the crossroads, one block at a time.  All of a sudden, she notices corners and the geometry of the street layout.  "I always thought the blocks went in a circle.  I didn't know they were squares."  The things she loves go on the map (friends' house, stone pig) as well as the things that 'used to' frighten her.  Her long battle with anxiety has its landmarks as well.

It may not be to scale, but when we go out again this afternoon to follow our map, the issue of scale might come up.  I'm also pretty sure we didn't get all the streets on there especially at the end of our route, but next time we'll bring paper and make some notes as we walk.

Mapping the familiar twists and turns and landmarks of our neighborhood -- bodies first, memories second, paper and pencils third.  I marvel at the human brain inside my six year old daughter's head that is so driven toward representation of her experiences and activities; driven toward it even though she is still just learning to decode print and write using 'the rules' .

She makes maps of other kinds, too.  Sewing "patterns", also not to scale, but clearly a sequence of steps mapped out:

I recently read a fascinating article in the New York Times about teachers taking their young students on walking field trips as a way to develop literacy.  This kind of activity is literally a step in the right direction.  Without concrete, kinesthetic, physical experiences like these, no child can fathom the meaning behind the marks on the page or develop full mastery of the human brain's greatest gifts. The order needs to be sensory experience / memory / symbols, not the other way around.

Math Books for Cats

I don't know for sure, but I suspect that every kid holds in his or her heart a metaphor or identity that can open the door to learning.

With my kid, you don't have to dig too deeply.  If it's a narrative that includes cats, she's interested (except with the Clan series -- too many kitties getting hurt make her crazy).  She is a cat, you know.  She started out a kitten at the age of two and now she's a cheetah (to account for the size of her six year old self).  Maybe you know a kid or two like her?

It's amazing how much you can learn through cats.  Interested in pioneer life?  No problem, there's the short chapter book called Pioneer Cat.  For a cat-led adventure through gripping transitional moments in world history, try Time Cat by Lloyd Alexander.  Flying cats?  The Catwings series by Ursula K. Le Guin is just the ticket.  Cookie's Week is perfect when you're learning to read.  Cross-species communication is covered in Jean Craighead George's How to Talk to Your Cat.  And, the cat book lover's ultimate cat book, Dewey: There's a Cat in the Library by Vicki Myron.

So, it probably comes as no surprise that I love any chance to work math into the cat obsession lifestyle.  Here are three books that have a special place in my heart. 

My very favorite cat and math book is Five Creatures, by Emily Jenkins.  It's about the similarities and differences (attributes!) between the members of a lovely little family. 

"Five creatures live in our house," it begins, "Three humans and two cats.  Three short, and two tall....Three with orange hair, and two with gray."  We read this book when my daughter was in preschool and it was fun for both of us to look at the pictures to see who matched each description.  The categories of family attributes are not always straightforward, which makes this a wonderfully interactive read.  I am planning to bring it out again and see how it looks through my daughter's now six-year-old eyes.

The tag line for One Hungry Cat by Joann Rocklin is "A greedy cat learns division."  When we first found it we read it over and over and over, giggling every time.  I'm going to go back to the library and get it again since we're heavy into arithmetic these days; it's got an introduction by Marilyn Burns, and a bunch of activities created by her to go with the story.  We play (and love) another Marylin Burns-created math activity using Cuisenaire rods called "Build What I Have" so I have a feeling there are some rich resources there.

So Many Cats! is also a favorite.  It's a straightforward story of a growing family of cats, but the rhyming text is musical and fun to read.  If you're a cat lover or, indeed, a real cat, you will read this with great affection for every new cat that joins the story.

If you have suggestions for more cat and math books to add to our list, both the kid and I would be thrilled to hear them! 

Hundreds Happiness!

Okay, I'll admit that when looking at a hundred's chart I've had the thought, "What's the big deal?"  I mean, the kid learns to count to one hundred and that's pretty much all there is too it, right? 

I still had that thought when I read Julie's post over at Craft Knife about her love of hundred's charts and her kids' love of the game 'Roll to 100'.  But, since Julie was so enthusiastic about it all and since we've been using dice for math games lately, I thought I might look into it.  Maybe the kid would be interested in coloring in the hundreds chart that way? 

She loved it!  In fact we played the game twice!  The second time we played she got all fancy and wanted to color in the chart using 'rainbow order.'

I think this must have been the first time she'd seen a chart like that.  I know they did a lot with counting to one hundred in kindergarten; I may be wrong but I don't remember seeing a chart like this in the classroom.  Anyhow, after a couple games with the dice I wanted to bump it up a little, and I remembered that Let's Play Math has a great post about twenty things you can do with a hundreds chart. 

From there I found a link there to some printables, including partially filled in charts where the kids can finish filling in the numbers.  Frankly, I was still dubious.  I wondered, "How hard is it really, to fill in the chart?"  I printed them out anyhow on the off chance I'd find a way to use them with the kid.

That was last night.  Today the kid had a leftover Valentine sticker that looked like a gold medal and she was searching for something to 'win'.  I said, "Wanna play some games with me?"  and she said, "Why don't you give me a math test and then I'll win this gold medal!"

Perfect!

I said, "Well, why don't we do something with the hundreds chart again, but this time I have a couple different options for you.  Do you want the one that's already filled in or one that's partially empty?"

She picked the partially empty one and, as we sat down, I did have the fleeting panic thought, "What am I going to do with this?!?"  I started with the already filled in three and said, "What comes before three?  Can you fill in those numerals?"  Then I noticed the tens all went down the right hand column.  I knew that she loved skip counting by tens, so we started there.

"What do you notice about this column?" I asked, and then the fun began!

Over the course of about 40 minutes, which is amazing for her, we alternated filling in columns and rows.  Since she knows skip counting by fives, we did that column next, but quickly realized that even in the five column you don't count by fives!  Obviously, I did not spend enough time with this chart when I was a kid. 

Anyhow, after figuring out what really needed to happen we tried the one's column.  I asked her, "This column starts with one, and the next number below is eleven.  We know now that when we go down the column, each number is ten more then the one before, so what number comes next in the box below eleven?"  It took a few minutes to establish an understanding of the pattern, and I used words like "Three tens and a one, four tens and a one, etc." to try and emphasize place value a little.  She only put up with that for about a minute at which point she asked me to stop talking so she could figure it out herself!

Initially she found filling in rows easier, because all you do is increase by one, but I encouraged her to do columns too.  At some point she exclaimed, "There's a pattern to this!" and happily filled out the rest of the chart column by column.   About two thirds of the way to completion she gushed,

"I love this.  I feel like I'm in the chart!"

In the end, when I look at the completed chart I'm still sort of thinking "What's the big deal?" but, watching her figure things out today, I know the meaning is in the creating.  There were a bunch of different, mostly empty chart printables that I printed out, and I'll leave those lying around and see what happens next.

Symmetry Artist: Exploring Attributes Through Design

I recently discovered how important the practice of identifying and describing attributes really is to math learning, especially at the elementary level.  Learning to discern similarities and differences develops mathematical thinking skills that can be used at all levels and topics within mathematics. 

Despite the thrill of discovering how this kind of thinking is used in my program Math in Your Feet, I was left with lingering questions about the differences between identifying attributes and using attributes in a design process.  I suppose they are two sides of the same coin, but I can't help thinking that being able to choose from an inventory of possibilities is the preferable skill-building activity in the long run.

I tested my theory on myself and my six year old daughter by using the Symmetry Artist at Math is Fun.  Maybe you've seen this before?  Check out all the attributes you can choose from to make your symmetry designs:

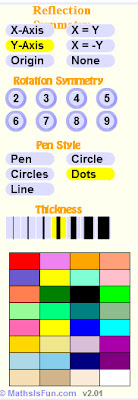You can choose between reflection or rotation symmetry, with six to eight choices in each category.

Your pen has five choices.

Seven thicknesses.

And many, many colors.

There's a lot to choose from here, but the tool is easy to use, so you can easily change your mind and start over, or take out your last move or series of moves. 

While you experiment and play around you are also noticing relationships between the lines and shapes you make and observing the structure of the final design.  The addition of color serves to increase the complexity and interest in both the process and the product.

I suppose the difference between identifying attributes and using attributes is that one is a more closed process than the other.  I'm thinking that with a set of attribute blocks, for example, although you are learning to discern differences and similarities, there are really only right and wrong answers.  The benefit of this kind of activity is that you are actively using math vocabulary: thick/thin, large/small, circle, square, triangle, edges, etc.  This is all very useful but, as I said, a somewhat closed process in terms of inquiry.

In contrast to 'compare/contrast/identify' there's the process like the one you use in Symmetry Artist. Instead of simply identifying attributes, you are using this skill in context while thinking mathematically in an active way -- you are actually 'doing' mathematics.  By this I mean you are asking questions ("What would happen if I started my circle here?  What would the same design look like with nine iterations instead of four?  How'd that pentagon get there?"), experimenting with and analyzing your 'answers' (designs), erasing your answers, starting over, printing out the answers you like, asking more questions.... This is the creative process in action; it is also mathematics in action.

I love Symmetry Artist because it is a beautiful and fun way to play around with, learn about, and compare how lines, shapes, and iterations interact within these two symmetries.  Below I've put just a few of the designs my daughter and I recently made. 

As a first grader, my kid uses this tool primarily for exploration.  I started by explaining the different categories, but not much more, and she jumped in from there.  I, on the other hand, being aware of just how many choices I had, jumped in but soon got overwhelmed with too many questions which led to too much erasing and/or starting over, resulting in pretty much nothing to show for my efforts!  That didn't stop me from noticing a few things, however.  Take a look at what we did, see what you think and then go try it yourself! 

Here's my daughter's first design.  Notice that she set it for rotation, 'eight', pen, one color, and a medium thickness.  She 'drew' with abandon, and I was thrilled with what resulted, mostly because I would have never thought to do it that way!  As you'll soon see, my initial approach was a bit more measured.

Her second design was inspired by the first.  "I want to draw a sun!" she said.  I don't know if you can see it, but she started with 'four' red, then 'nine' red, then 'nine' yellow.

Here's the one I made as an example to show the kid what you can do with the tool.  I used 'five', circle, and some variations in thickness and color.  I love the almost-pentagon in the center where the five big circles cross.

The one thing during my experimentation that really thrilled me was that I noticed a difference between the process of drawing a design with a line of symmetry compared with what happened while using 'two' rotation.  Can you see it?

I know what it looks like, and how to describe it, when a two-person team transforms their percussive patterns using both kinds of symmetries, but there was something about using Symmetry Artist that made it stand out to me in a different way.  You are actually drawing one design and the multiples show up automatically.  There was something about seeing it happen in real time (moving patterns!) that I would not have noticed if I had been drawing it by hand, one reflection or rotation iteration at a time.  If I had been doing it that way (pencil and paper) I probably would have noticed something else altogether.

This is all just more evidence that you really do need multiple opportunities to observe and work with a math concept in a number of different situations to really understand it.  In the end, I think that both the act of identifying attributes and and the act of using attributes in a design process (choreography, visual art, tangrams, etc.) have something to offer each other. 

Because I am a teaching artist, dancer and musician, I am coming at math education from a different direction than many.  I am also a big picture learner, so putting math in context makes a great deal of sense to me.  What I am still thinking about are things like: When is it important to just teach math as math?  When do you move on to reflection on and representation of the math you've discovered during an open-ended exploration?  These are the questions that quite literally keep me up at night, and one reason that it's taken me so long to get this post the way I wanted it.  I suppose I may be overthinking things, but I really am curious about all this.

What's your experience with attributes?  I'd love to hear what you think about all this!

Open Ended

I just realized that a lot of my posts lately have been about making mathy things out of open ended materials: straws, pipe cleaners, craft sticks, rubberbands, paper, glue.  It's made me think about when I teach Math in Your Feet, how fourth and fifth graders almost can't believe it when they've made up their own eight-count pattern out of nothing more than three categories of movement-based attributes.  One child even said to me, during our end-of-week reflection time: "I didn't know I could make anything."   Heavy sigh.

This ad from 1981 reads:

"Have you ever seen anything like it?  Not just what she's made but how proud it's made her?  It's a look you'll see whenever children build something all by themselves.  No matter what they've created."

There's a lot this ad says to me, but the very most important thing is that:

It is imperative that we give our children, and our students, a chance to explore and discover at least part of what they learn ON THEIR OWN, ideally with open-ended materials and perhaps a very casually introduced question.  This doesn't mean that the learning environment becomes chaotic, or that teachers aren't needed.  Structure and forethought are still useful but, in this case, they become the background against which children employ their own desires to the materials at hand. 

We need to trust that kids can figure things out for themselves sometimes, and that the best learning often happens as a result of a question and the self-motivation to find an answer that suits them in the moment. 

Shut the Box, aka Beat the Sailor: Fun with Number Combinations

"Wanna play UNO?" 

"No!"

"How about Shut the Box?"

"No! I want to go to finishing school!"

"I'm not sure we have one around here."

"But we can do it at home."

"True.  I know!  Every fine young lady needs to know how to outsmart a sailor."  Noooo...there was nothing at all off color implied here, it's just that... "Shut the Box is the sailor's game, you know.  Part of your finishing could be to learn how to beat them at their own game!"

"Why?"

"Because fine young ladies also need to learn to be smart and strong and know how to think for themselves."

"Okay!  Let's play!"

And, in case you didn't know, Shut the Box is fabulous for practicing combinations of ten [Edit: That's not what I meant!  I meant finding different ways to make the number you roll with the two dice.  Duh!].  And then you add up the leftover points, which can go into the twenties if you haven't yet figured out all the strategies.  (She's been doing all this in her head, sometimes with fingers for the larger numbers.)

And...once she is really strong with tens we can move on to a game that didn't quite work a few weeks ago -- 'Tic Tac 15'.  The stronger she gets at adding, the more adept she is at skip counting and figuring out her own answers for questions that require multiplicative thinking.

For instance, we were at the grocery store the other day, walking through the wine section (I know, I know, this all has a sordid cast to it, but really, it's all circumstantial and quite innocent).  There was a case of bottles and a sign that said "$10.99 a bottle".  I didn't even notice it until, unbidden, she started counting, "Ten, twenty, thirty...."

She was trying to figure out how much the whole case cost!  Next time I'll try to keep my wits about me and mention that $10.99 is actually very close to $11.00 and then I show her the fun in skip counting by elevens!

p.s. In case it isn't clear, I'm taking the role of the sailor.  I'm also the coach -- I've been walking her through the strategy of shutting the higher numerals first (sort of like in UNO) so you don't get stuck with those points at the end, but on my turn I play more erratically so that she wins.  For now, anyhow.   At some point we'll move on to timed rounds or something even more cutthroat.  It is a sailor's game, after all.

A Big Discovery

The kid and I were playing around with tangrams the other day and -- all of a sudden -- I had an Aha! moment.  It was a chain of connected thoughts and realizations which provided clarity around an answer I've been hunting down for the last fifteen months.  Yeah, I know, this big!  Here's how played out:

I recently read a post by Shelisa at Think Magnet which I found at the Love2Learn2Day Math Monday Blog Hop.  The post was about a brilliant game Shelisa plays with her kids every time the family sits down to a meal. 

I was completely impressed with the game because not only did it grow out of a spontaneous observation by one of her kids (my favorite kind of learning) but she was then inspired and able to turn the moment into a wonderfully complex and endlessly interesting activity.

I can't really do justice describing the game here; you'll have to go see for yourself and you'll be glad you did!  But, the upshot is that the game is all about attributes and learning how to discern differences and similarities.  It is also about just how inspiring a playful approach to learning can really be. 

For the most part, I've been following my own kid's interest and questioning related to math over the last six months, an inquiry which has focused on measurement, maps, number patterns, and geometry discoveries.  Reading Shelisa's post I started wondering how I might incorporate it more directly into our own math explorations.

So there I was, later that day, mulling all this over at a semi-conscious level in the back of my brain while sitting on the kitchen floor with my daughter.  We had just re-discovered a whole box of tangrams, with four or five puzzles all mixed together. 

"Look Mama!" the kid exclaimed, "I made a parallelogram out of triangles!  And I can use two more triangles to make it into a rectangle!" 

At the time I was playing around with building squares and I decided to start building onto her rectangle.

"Oh, look!" I said, "I can make a big square out of two triangles.  And I can make a second square out of four smaller squares.  If we make a third square and add it on, we'll have made your rectangle even larger!  How can we make the third square differently from the first two?"

And, in my mind, I said: We can play around with position, size and color.  Adding attributes like these increases complexity and interest...

And that's when it hit me.  How many ways can you make...?  That's the question I had been asking the kid about the number twenty or the number ten.  And here I was asking a similar question (How can you make the third square different from the first two?) about combinations of shapes, and colors, and sizes. 

Attributes and combinations. 

I ask this type of question in Math in Your Feet too: Which of these movement variables will you choose as you create your four beat pattern?  How can you make your second pattern different from your first?  To help them find their 'answer', students use a tool I created called Jump Patterns to choreograph their own foot-based percussive dance patterns.  Jump Patterns are created by working with the elements of a percussive dance step (the related math term being 'pattern unit').  Take a look at the chart I use in the classroom:

Students use this chart to experiment with what I have always called Movement Variables, except now I realize that, in the math sense, they're a collection of....attributes!

For the classic set of attribute blocks it's five shapes, three colors, two thicknesses and two sizes.

In Math in Your Feet kids choose from five foot positions, six types of movement, and six directions to create each of the four beats in their Pattern A, and then they make choices again when they choreograph Pattern B.  There are two other categories to work with as well, including tempo and starting position. 

Here's why it's a big deal:

The math topics in Math in Your Feet have always been clear to me: concrete, kinesthetic experience with spatial reasoning, combinations, congruence, transformation, reflection, and rotation.  These are the things kids and their teachers know are being taught.  They've always been the 'selling points' of the program because they are easily recognized and understood as 'math'.  

But, after years of  working out connections between these topics and percussive dance I knew there was more going on than simply learning 'about' math.  My hunch was that there was some real mathematical thinking going on, I just needed to figure out where it was occurring and how to explain it.

This hunch was one reason I embarked on my current math quest (chronicled in this blog over the last fifteen months).  I've been working hard to figure out what it means to 'do' math.  And now, my new understanding about the nature and purpose of identifying attributes in elementary math education has provided at least part of the answer:

When children are able to identify the elements (attributes) that they have used in their creative dance work they are thinking mathematically.  When they use this understanding to analyze and critique others' creative work they are thinking mathematically.  Attributes are 'charactaristics of an object or a shape' and I'm confident that this definition is broad enough to include moving pattern units as well.

I am struggling at the moment to articulate my thoughts about the differences between identifying attributes in a traditional math education setting vs. choosing attributes in a creative or design process.  But, no worries!  After more than a year of asking, surfing, conversing, reading and learning, I feel like I have won some kind of prize!  And, thanks so much to everyone who is sharing this journey with me.

p.s. If you want to learn more about Jump Patterns, here's a link to an article I wrote that details the whole story of what they are, how I developed the tool, and how they are used in the classroom.